
Olleh:s teorisamling - Harmonisk svängning
Harmonisk svängning
En harmonisk svängning hos en partikel är en periodisk rörelse där partikeln svänger fram och tillbaka kring
ett jämviktsläge.
Exempelvis kommer en kula som hänger i en fjäder att utföra harmoniska svängningar.
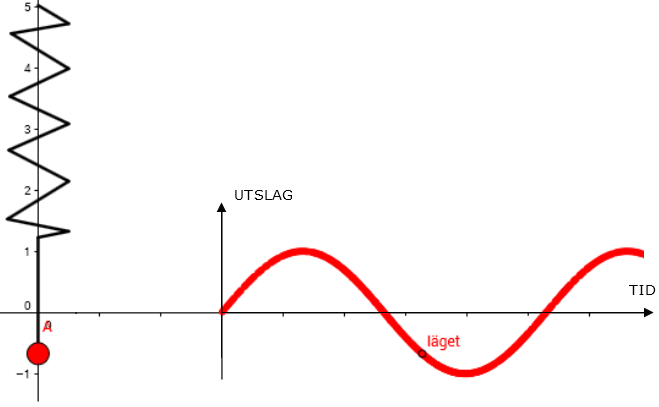
Kulan svänger med varierande hastighet från ett högsta läge, passerar jämviktsläget och kommer till ett lägsta läge
och rör sig uppåt, passerar jämviktsläget och når högsta läget. Denna rörelse upprepas hela tiden.
Skillnaden mellan högsta och lägsta läget är 2A där A är amplituden.
Avståndet från jämviktsläget och ena ändläget är således amplituden 1A.
Kulan har i varje läge en hastighet v och en acceleration a som ges av sambanden:
s = A·sin(ωt)
v = ωA·cos(ωt)
a = -ω²A·sin(ωt)
där A är amplituden, ω är vinkelhastigheten och t är tiden i sekunder.
Om vinkelhastigheten ω ökas med 2π har partikeln rört sig från ett läge till nästa gång samma läge inträffar.
Tiden som har gått under denna förflyttning är tiden för en period T.
Flöjande samband råder mellan vinkelhastighet ω och periodtid T:
ω = 2πT
Bestämning av ω
Enligt Hookes lag kommer en fjäder som blir utdragen att motverka utdragningen med en kraft F som är proportionell mot fjäderns förlängning Δx.
F = - k·Δx
Men enligt Newtons 2:a lag kommer ett föremål som påverkas av en resulterande kraft F att accelereras:
F = m·a
För den svängande kulan gäller :
F = - k·Δx
där Δx = A·sin(ωt)
F = m·a
där a = -ω²A·sin(ωt)
Sätt krafterna lika som ger:
-k·Δx = m·a
-k·A·sin(ωt) = -m·ω²A·sin(ωt)
Förenkling ger:
k = m·ω²
Lös ut ω:
ω = √km
Svängningens energi
Partikeln har i varje ögonblick en rörelseenergi och fjädern har en potentiell energi.
När partikeln är i ett av vändlägena
har den ingen hastighet och därmed ingen rörelseenergi. Fjädern har blivit hoptryckt eller utdragen maximalt och alla
energi finns lagrad i fjädern.
Vid passagen av jämviktsläget har partikeln maximal hastighet och fjäderkraften på partikeln är noll.
Energin kommer att pendla mellan maximal rörelseenergi och maximal potentiell energi.
Den maximala rörelseenergin med v = vmax = ωA (cos(ωt) = 1)
Ek = 12 m(vmax)² = 12 m(ωA)² = 12 m√km ·
√km·A2 = 12 kA²
Den maximala potentiella energin då fjädern är intryckt max dvs. sträckan A:
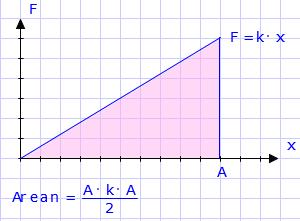
Ep = 12 ·A·kA = 12 kA²
Energin vid en godtycklig punkt x = Asin(ωt) och v = ωAcos(ωt):
Etot = Ek + Ep = 12 mv² + 12 kx² = 12 m[ωA·cos(ωt)]2 + 12 k[Asin(ωt)]2
Etot = 12 mω²A²[cos(ωt)]2 + 12 kA²[sin(ωt)]2
Men då ω² = km och sin² + cos² = 1
blir uttrycket:
Etot = 12 m kmA²[cos(ωt)]2 + 12 kA²[sin(ωt)]2 = 12 kA²
upp




