bilder/logoolleh.gif

Olleh:s teorisamling - Komplexa tal

home

Imaginära enheten

bilder/komplexatalplan.GIF

Det finns inga reella tal som är lösningar till ekvationen
x² = -1

För att lösa ekvationen måste man utvidga de reella talen.
De reella talen kan ses som alla tal på x-axeln.
Man inför en ny dimension, den imaginära dimensionen, som är vinkelrät mot x-axeln. Man får ett tvådimensionellt talplan, ett komplext talplan.
Ett komplext tal kan representeras av en punkt i det komplexa talplanet.

Ett komplext tal består av en realdel längs x-axeln och en imaginärdel längs y-axeln.
x-axeln kallas reella axeln och y-axeln kallas imaginära axeln.
Man inför en imaginär enhet i som har egenskapen
i2 = -1
Ett komplext tal kan skrivas a + bi.
där a och b är reella tal.
I bilden är de komplexa talen 5 + 2i och 3 - 2i utritade.

Addition och subtraktion

Vid addition adderas realdelarna för sig och imaginära delarna för sig.
z1 = a + bi
z2 = c + di

z1 + z2 = (a + bi) + (c + di) = (a + c) + (b + d)i

Exempel:
(2 + 3i) + (5 - 4i) = (2 + 5) + (3 - 4)i = 7 + (-1)i = 7 - i

Subtraktion går till på motsvarande sätt
z1 = a + bi
z2 = c + di

z1 - z2 = (a + bi) - (c + di) = (a - c) + (b - d)i

Exempel:
(2 + 3i) - (5 - 4i) = (2 - 5) + (3 - (-4))i = -3 + (3 + 4)i = -3 + 7i

Multiplikation

Multiplikation av två komplexa tal sker på samma sätt som multiplikation av två parenteser.
z1 = a + bi
z2 = c + di

z1 · z2 = (a + bi) · (c + di) = a·c + a·di + bi·c + bi·di =
(ac + bdi²) + (ad + bc)i = (ac - bd) + (ad + bc)i
eftersom i² = -1

Exempel:
(2 + 3i) · (5 - 4i) =
2·5 + 2·(-4)i + 3i·5 + 3i·(-4)i =
(10 + (-12)i²) + (-8 + 15)i =
(10 + 12) + (-8 + 15)i =
22 + 7i

Absolutbeloppet

bilder/komplexatalplan-pil.GIF
De komplexa talen representeras ofta av pilar som utgår från origo.
I bilden till höger visas de komplexa talen z1 = 5 + 2i och z2 = 4 - 3i som pilar.

Pilarnas längd visar de komplexa talens storlek.
Pilens längd kallas absolutbeloppet av det komplexa talet z,
där z = a + bi.

|z| = √a² + b²

Så är t.ex. |z2| = √4² + (-3)² = 5

Cirkel i komplexa talplanet
|z| = absolutbeloppet av z betyder hur långt från origo som z ligger i det komplexa talplanet.
Detta kan tydligare skrivas
|z - 0| som kan tolkas som avståndet mellan z och talet 0.
|z - 0| = 3 betyder alla tal z som ligger 3 enheter från talet 0 (origo). Dessa tal ligger på en cirkel med radien 3 och medelpunkt i origo.

bilder/cirkel-koplex.GIF

|z - (1 + 2i)| = 3 betyder alla tal z som ligger 3 enheter från talet (1 + 2i). Dessa tal z ligger på en cirkel med radien 3 och har medelpunkt (1 + 2i).

|z - (1 + 2i)| < 3 betyder alla tal z som ligger mindre än 3 enheter från punkten (1 + 2i). Dessa tal ligger på cirkelytan innanför cirkeln med radien 3 och medelpunkt (1 + 2i).

|z + 1 + i | kan skrivas om till |z - (-1 - i) | och då inser man att
|z + 1 + i | = 2 betyder alla tal z som ligger 2 längdenheter från
punkten (-1 - i ). Dessa tal ligger på en cirkel med (-1 - i) som medelpunkt och cirkelradien = 2.

Konjugatuttrycket av z

bilder/z-konjugat.GIF

Det komplexa talet z = a + bi har ett konjugatuttryck
z-konjugat som skrivs
z = a - bi

I det komplexa talplanet åskådliggörs det komplexa talet
4 + 3i som en punkt (4, 3)
och konjugatet 4 - 3i blir punkten (4, -3).
Konjugatet z är en spegelbild av z med x-axeln som spegel.

Det gäller att

z · z = (a + bi)(a - bi) = a² + b²

är ett reellt tal.

Man kan också se att

|z| · |z| = z · z = a² + b²

Division

Division av komplexa tal är lite mer komplicerad än multiplikation.
z1 = a + bi
z2 = c + di
a+bi
c+di
Genom att förlänga med nämnarens konjugat får man en reell nämnare. 
a+bi = (a+bi)(c-di) = (ac-bdi²)+(-ad+bc)i = 
c+di   (c+di)(c-di)          c²+d²

(ac+bd)+(-ad+bc)i
     c²+d²
Exempel:
(5+3i) = (5+3i)(3+4i) = (15-12)+(9+20)i = 3+29i =
(3-4i)   (3-4i)(3+4i)        9+16          25
= 0.12 + 1.16i

Argumentet för z

bilder/argz.GIF

Ser man det komplexa talet z = a + bi som en vektor från origo till punkten (a, b) i det komplexa talplanet är argumentet för z vinkeln mellan positiva Reella Axeln (x-axeln) och riktningen till punkten (a, b).
Vinkeln kan beräknas med

arg(z) = tan-1(b/a)

Exempel:
Bestäm arg(z) om z = 5 + 3i (se figur).
arg(z) = arg(5 + 3i) = tan-1(3/5) = 31°

Polär form

bilder/polarform.GIF

Det komplexa talet a + bi kan beskrivas med trigonometri.
Räknat från origo ligger talet |z| enheter bort och vinkeln mot x-axeln ges av arg(z) = φ.
Koordinaterna för z blir då
a = Re(z) = |z| · cos φ
b = Im(z) = |z| · sin φ

z kan då skrivas:

z = a + bi = |z| · cos(φ) + |z| · sin(φ)·i = |z| (cos φ + i sin φ)

Exempel:
z = 3 + 4i
φ = tan-1(b/a) = tan-1(4/3) = 53°

|z| = √a² + b² = √3² + 4² = 5

z = 5(cos 53° + i sin 53°)

Multiplikation i polär form

Det komplexa talet z = a + bi kan skrivas i polär form som z = r (cos φ + i sinφ)
där
r = |z| = √a² + b² är längden av z och
φ = arg(z) är vinkeln mellan x-axeln och riktningen från origo till z

z1 = a + bi = r1(cos φ + i sin φ)
z2 = c + di = r2(cos θ + i sin θ)

z1 · z2 = r1 (cos φ + i sin φ) · r2 (cos θ + i sin θ)
z1 · z2 = r1 · r2 (cos φ + i sin φ) · (cos θ + i sin θ)

som blir sedan parenteserna multiplicerats ihop:

z1 · z2 = r1 · r2 (cos φ · cos θ + cos φ · i sin θ + i sin φ · cos θ + i sin φ · i sin θ)

Samla ihop realdelarna för sig och imaginärdelarna för sig:

z1 · z2 = r1 · r2 (cos φ · cos θ + i sin φ · i sin θ + i (cos φ · sin θ + sin φ · cos θ )

Sätt i² = -1 ger:

z1 · z2 = r1 · r2 (cos φ · cos θ - sin φ · sin θ + i (cos φ · sin θ + sin φ · cos θ )

Med hjälp av formelsamlingen och additionsformlerna för sinus och cosinus ser man att den röda texten kan ersättas med
cos(φ + θ)
och den blå med
sin(φ + θ)

z1 · z2 = r1 · r2 (cos(φ + θ) + i sin(φ + θ))

Uttrycket kan generaliseras till fler faktorer så t.ex.

z1 · z2 · z3 = r1 · r2 · r3 (cos(φ + θ + ρ) + i sin(φ + θ + ρ))

Division i polär form

z = a + bi = r·(cos φ + i sin φ)
w = c + di = s·(cos θ + i sin θ) 
z = a+bi = r(cos φ+isin φ)
w   c+di   s(cos θ+isin θ)
Förläng med konjugatuttrycket: 
z = a+bi = r(cos φ+isin φ)(cos θ-isin θ)
w   c+di   s(cos θ+isin θ)(cos θ-isin θ)
Täljarens parenteser kan skrivas om till
(cos φ · cos θ + cos φ · (-i sin θ) + i sin φ · cos θ + i sin φ · (-i sin θ))
Samla ihop de imaginära delarna
cos φ · cos θ + i sin φ · (-i sin θ) + i (cos φ · (-sin θ) + sin φ · cos θ)
tänk på att i² = -1
cos φ · cos θ + sin φ · sin θ + i (-cos φ · sin θ + sin φ · cos θ)
Formelsamlingen ger att den röda realdelen kan ersättas med
cos(φ - θ)
och den imaginära blå delen med
sin(φ - θ)

Utvecklar man nämnaren
(cos θ + i sin θ)(cos θ - i sin θ) =
cos θ · cos θ + i sin θ · (-i sin θ) + i (cos θ · (-sin θ) + sin θ · cos θ)
tar imaginärdelarna ut varandra och realdelarna blir 1. (cos²θ - i² sin²θ = 1)

z / w = r / s · (cos(φ - θ) + i sin(φ - θ) )

De Moivres formel

Med de Moivres formel kan man beräkna zn eller n√z där n är ett heltal.

Skriv z på polär form.
z = r · (cos(φ) + i sin(φ))
Då blir

zn = (r · (cos(φ) + i sin(φ)))n = rn · (cos(n·φ) + i sin(n·φ))


Om z = r · (cos(φ) + i sin(φ))
så blir

n√z = n√r · (cos((φ + k·2π)/n) + i sin((φ + k·2π)/n))

där k är ett heltal. För att få de n olika rötterna ska k genomlöpa värdena 0 till n-1.
upp

Eulers formel

eiv = cos v + i·sin v

Bevis för Eulers formel

Exponentialfunktionen ex kan serieutvecklas till en sk. Taylor-serie:

ex = 1 + x/1! + x2/2! + x3/3! + x4/4! + x5/5! + x6/6! + x7/7! + ...

(3! uttalas tre-fakultet och betyder produkten av de naturliga talen 1·2·3.
4! = 1·2·3·4.)

På liknande sätt kan sin x och cos x utvecklas:

sin x = x − x3/3! + x5/5! − x7/7! + ...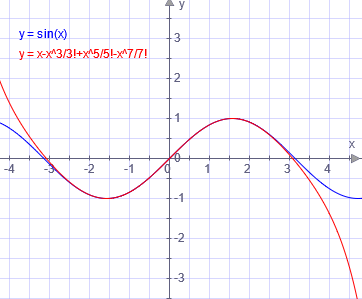

bilder/sinx-serie.png

sin x (blå) och serieutveckling med 4 termer (röd)
Kurvorna är nästan identiska mellan -3 och +3.

cos x = 1 − x2/2! + x4/4! − x6/6! + ...

Sätter man i uttrycket ex istället exponenten till ix blir det:
eix
där x är ett reellt tal.

eix kan serieutvecklas till:

eix = 1 + ix/1! + (ix)2/2! + (ix)3/3! + (ix)4/4! + (ix)5/5! + (ix)6/6! + (ix)7/7! + ...

Med i2 = -1 blir detta:

eix = 1 + ix/1! − x2/2! − ix3/3! + x4/4! + ix5/5! − x6/6! − ix7/7! + ...


Skriver man om termerna och bryter ut i får man:

eix = (1 − x2/2! + x4/4! − x6/6! + ...) + i( x/1! − x3/3! + x5/5! − ix7/7! + ...)

som kan skrivas:

eix = cos x + i· sin x
Läs mer
home